![]()
ISSN 2379-5980 (online) DOI 10.5195/LEDGER.2024.389
RESEARCH ARTICLE
Market Neutral Liquidity Provision
Basile Maire,∗† Marcus Wunsch‡
Abstract. Automated Market Makers with concentrated liquidity have to date achieved market dominance among competing spot trading AMM models in Decentralized Finance. We shift the prevalent research focus on liquidity providers’ loss metrics, such as Impermanent Loss or Loss-Versus-Rebalancing, to a market neutral strategy. We derive a hedge portfolio which allows for concentrated liquidity provision while maintaining market neutrality. We present an example of the hedge portfolio and highlight the practical restrictions. The hedge portfolio consisting of options and futures requires a significant capital outlay compared to the amount of liquidity provided, but typically earns carry from futures contango.
![]()
∗ 0xba512e9eddb0a80793e54c6c77577c3db743ea97
† B. Maire (basile.maire@quantena.tech) is co-founder of Quantena AG.
‡ M. Wunsch (marcus.wunsch@zhaw.ch) is a Senior Lecturer at ZHAW School of Management and Law.
![]()
The initially low throughput of blockchains necessitated a unique spot trading model that differs from the traditional order-book approach. This led to the development of Automated Market Makers (AMMs), which are smart contracts that programmatically determine the exchange rate between two cryptocurrencies (or tokens). In order-book-based trading venues, market makers post limit orders, whereas in AMMs, liquidity providers lock tokens into a smart contract, called the liquidity pool, to earn trading fees. Traders can swap one token for the other, the exchange rate being determined by the trading function. Such trades result in changes in the composition of the liquidity pool.
The assessment of the liquidity provider’s portfolio value has attracted considerable interest both among practitioners and academics. In the context of the cryptocurrency bull run and the surge in retail activity observed in 2021, the main attention has been on “impermanent loss”, which is the (relative) difference in the liquidity provider portfolio value compared to a buy-and- hold strategy. That is, as the price of the first token changes in relation to the second token (for example as the value of BTC increases in relation to a stable USD-token), the liquidity provider portfolio value experiences a smaller increase in value compared to a buy-and-hold strategy, disregarding fees earned in the liquidity pool. In the subsequent bear market, and with, arguably, the gradual influx of professional liquidity providers, we argue that hedging the dollar-value of the liquidity provider portfolio has gained more attention.
Among the myriads of AMM types, concentrated liquidity AMMs are the most prominent type of AMMs at the time of writing, measured by trading volume and liquidity provision, as evidenced in Table 3 in Appendix B. Given this dominance and the focus of the literature on impermanent loss (typically a concern for unbounded liquidity provision), we see a gap in the literature for a rigorous derivation of the hedging portfolio for the liquidity provider in concentrated pools, coupled with practical applicability. Liquidity providers who hedge their impermanent loss follow (by definition of impermanent loss) a buy-and-hold strategy. We shift the focus towards a market-neutral strategy where the goal is to keep the numéraire value of the portfolio constant while earning interest from trading fees, instead of profits from speculative investing. We contribute to the literature by deriving a numéraire hedge for the most prominent AMM type, concentrated liquidity for constant function markets (e.g. Uniswap v3), in a more rigorous framework than previously published (cf. Clark (2021)1). Moreover, we provide an empirical example of such a hedge using data from Deribit, a crypto options exchange, and report practical limitations.
The resulting hedging strategy consists of a portfolio of long straddles, enclosed by a long and short synthetic position in the underlying that we construct with options (the long synthetic corresponds to a long call and a short put at the same strike). While in theory the hedge is constructed with a portfolio of a continuum of option strikes, we find that, based on our example hedge, only a few options are required for the hedge to be effective. If the margin of the hedge is held in the underlying such as BTC or ETH as on Deribit, the margin itself is to be hedged as well.
The difficulties in implementing the hedge result from the limited availability of options for cryptocurrencies affecting the choice of tokens, the minimal contract sizes, the range of liquidity provision, and the maturity of the hedged liquidity provision. The minimal option contract sizes render hedging for smaller liquidity provisions prohibitively costly. The hedger also faces a limited availability to write (i.e., sell) options. On Deribit, options are margined in the token itself (as opposed to a USD-stable token), and hence a hedge for the margin collateral is required. Either a perpetual future or a dated future is well-suited. Historically, short positions in perpetual futures on average earn funding rates,2 and short positions in dated cryptocurrency futures typically earn a carry,3 both of which are beneficial to our hedging strategy.
At maturity, the gain of the option portfolio corresponds to the loss of the LP position (or vice versa). The margin requirement for the options sold is non-negligible and locks up capital of about double the liquidity provision amount in our example. The collateral of the inverse options needs to be hedged too. However, the entire hedge portfolio, consisting of a portfolio of long and short options and a short future, earns carry from the future. The premia of the options sold exceeds the premia from the options bought and thus reduces the expense at trade initiation. A significant portion of the portfolio return stems from the futures carry (or, correspondingly, the perpetuals’ funding rates).
1.1. Spot Trading AMMs—A general class of AMMs are Constant Function Market Makers (CFMM), in which liquidity takers swap x units of the first currency for y units of the second currency in accordance with the equation
| $$\varphi(\tilde{x}, \tilde{y}, x, y) = \varphi(\tilde{x}, \tilde{y}, 0, 0)$$ | $$(1)$$ |
(see e.g., Mohan (2022)).4 The function \(\varphi\) is called the trading function and is increasing in each of its arguments. The arguments \(\tilde{x} > 0\) and \(\tilde{y} > 0\) represent the reserve amounts of the first and second currency in the pool at the time. When the trade amount \(x > 0\), this means a liquidity taker adds \(x\) units of the first currency to the pool to receive \(-y > 0\) units of the second currency from the LP (or vice-versa with \(y>0)\). AMMs were introduced by Bancor in 2017 and gained prominence with the implementation of Uniswap (v1 and v2). The trading function Bancor and Unsiwap employed is termed the Constant Product Market Maker, which prescribes that the post-trade product of the two reserve tokens equals the pre-trade value. Thus
| $$\varphi(\tilde{x}, \tilde{y}, x, y) = \sqrt{(\tilde{x}+ x) (\tilde{y}+ y)}$$ | $$(2)$$ |
together with Equation (1) holds. While Uniswap-type Constant Product Market Maker pools consist of two assets, Balancer extended the idea and created Geometric Mean Market Makers that comprise pools of several assets.5 Curve, a prominent example for Hybrid Function Market Makers, aims to provide sufficient liquidity with little slippage for stable assets.6 Despite its prevalence for stable pairs, Curve is less relevant for our study because the focus on stable pairs implies a stable value for the liquidity provider portfolio. Uniswap introduced concentrated liquidity with its version 3, the type of AMM we focus on in this study.
1.2 Literature—Constant Product Market Makers (CPMMs) have attracted considerable attention from practitioners and academics alike, see Mohan (2022).4 The research focus has so far been mainly on Impermanent Loss, which can be characterized as a manifestation of adverse selection risk that liquidity providers are exposed to (cf., e.g., Milionis et al. (2023)7). In fact, Fukasawa et al. “Weighted Variance Swaps” (2023) showed that Impermanent Loss is equivalent to selling a particular portfolio of European put and call options, and can thus be hedged statically by purchasing this option basket, assuming fees are not part of the pool.8 The analysis therein was generalized in Fukasawa et al. “Model-Free Hedging” (2023) by including fees, where the authors showed that Impermanent Loss can be super-hedged dynamically and that the shortfall versus a self-financing portfolio with the same constant weights vanishes (Loss- Versus-Rebalancing) if there is perfect competition among arbitrageurs;9 cf. also Milionis et al. (2023).10 While most of the impermanent loss literature focuses on Uniswap v2-type AMMs, Lipton et al. (2024) propose a unified approach to hedging impermanent loss for both Uniswap v2 and its next iteration, Uniswap v3, implementing concentrated liquidity provision.11 Clark (2020) derives a replicating portfolio for the liquidity provision portfolio of a Constant Product AMM, assuming vanishing fees.12
Our approach is related technically with the work of Clark (2021) and Deng et al.1,13 The latter derived the replicating portfolio for impermanent loss in concentrated CPMMs, the former derived a replicating portfolio for concentrated liquidity involving bonds and options.
Uniswap v3 is a constant function market maker in which liquidity providers deposit tokens for a given price range \(P_U\) to \(P_L\).14 The boundaries can be chosen at a discrete granularity, termed ticks. Within the ticks, the trading function is borrowed from Uniswap v2, that is, when swapping \(\Delta x\) tokens of token \(X\) (after fees), the amount \(\Delta y\) of token \(Y\)received (vice versa when adding \(\Delta y\) after fees) is given by
| $$\left(x^{(v)}+ \Delta x\right)\left( y^{(v)}+\Delta y\right) = L_i$$ | $$(3)$$ |
where \(L_i\) is a variable termed liquidity that is tracked for every price range \(i\) (between the ticks) and constant within a range as long as no additional liquidity providers enter or exit the pool. However, \(x^{(v)}\) and \(y^{(v)}\) that in v2 correspond to the global amounts of tokens \(X\) and \(Y\) are ‘virtual’ in v3 and derived from price and \(L_i\): \(L_i = \sqrt{x^{(v)}y^{(v)}}\), \(\sqrt{P} = \sqrt{y^{(v)}/x^{(v)}}\) The trading function is applied up to the tick boundary and continued with the different liquidity \(L_j\) belonging to the next range.
2.1 Liquidity Provision—With \(P_U\) and \(P_L\) the upper and lower tick prices for which the liquidity provider wants to offer liquidity, initial deposits, \((y, x)\), at price \(p\) are determined as specified in (6.29) and (6.30) of the Uniswap v3 Whitepaper:16
| $$ y = \left\{ \begin{array}{ll} 0 & P < P_L \\ \ell \left(\sqrt{P}-\sqrt{P_L}\right) & P_L < P < P_U \\ \ell \left(\sqrt{P_U}-\sqrt{P_L}\right) & P >P_U \end{array} \right.$$ | $$(4)$$ |
| $$x = \left\{ \begin{array}{ll} \ell \left(\frac{1}{\sqrt{P_L}}-\frac{1}{\sqrt{P_U}}\right) & P < P_L \\ \ell \left(\frac{1}{\sqrt{P}}-\frac{1}{\sqrt{P_U}}\right) & P_L < P < P_U \\ 0 & P>P_U. \end{array} \right.$$ | $$(5)$$ |
For a given “liquidity” \(\ell\), lower bound price \(P_L\), and upper bound price PU , the amount of token X, \(x\), and the amount of token Y, \(y\), are given by the above equation. In practice, the liquidity provider would, for example, specify the amount of token \(Y\), \(P_L\), and \(P_U\) and the amounts \(\ell\) and \(x\) would then be given by the two equations. The pool liquidity between \(P_U\) and \(P_L\) increases by \(\ell\), that is \(L_i \leftarrow L_i+\ell\) for all ranges \(i\) within \(P_U\) and \(P_L\). The Liquidity Provision positions stores the value \(\ell\). The value \(\ell\) remains constant, regardless of price changes, fees earned, and liquidity added by other participants. Fees in Uniswap v3 are kept outside the pool so that, together with \(\ell\) being invariant, the liquidity provision portfolio can be accurately valued without additional assumptions given a price \(P\), independent of the trading activity—unlike in v2.17
2.2 Liquidity Position Valuation—For a given position, the token composition of a given liquidity position varies with the price \(P\) as specified in Equations (4) and (5), in which all variables except \(P\) remain constant as the price \(P\) moves. For prices \(P\) above the upper limit \(P_U\), the liquidity provider only holds token \(Y\) (the numéraire token). For prices \(P < P_L\), the liquidity provider is left with only token \(X\).
We can now express the value of the liquidity position as a function of the price
| $$\left\{V(P) = y + x P \right.$$ | $$(6)$$ |
| $$= \left\{ \begin{array}{ll} \ell P (\frac{1}{\sqrt{P_L}}-\frac{1}{\sqrt{P_U}}) & P < P_L \\ \ell (\sqrt{P}-\sqrt{P_L})+ \ell (\frac{1}{\sqrt{P}}-\frac{1}{\sqrt{P_U}}) P & P_L < P < P_U \\ \ell (\sqrt{P_U}-\sqrt{P_L}) & P > P_U \end{array} \right.$$ | $$(7)$$ |
where the token value is expressed with numéraire \(Y\). The liquidity provider position can be dynamically delta-hedged with respect to the numéraire \(Y\) by entering a position of \(-\partial V(P)/\partial P\), the position negative delta. Clearly, the delta hedge, \(-\partial V(P)/\partial P\), corresponds to shorting the amount of token \(x\)that the liquidity provider owns for a given price \(P\), and therefore the delta coincides with Equation (5). In Appendix 3, we derive Delta and Gamma, and plot an example of the liquidity provision value as a function of price, delta, and token composition (Figure 4). The payoff \(V(P)\) superficially resembles that of a covered call option, an observation taken up by DeFi projects.18
We consider a liquidity provider entering at price \(P_0\) with token amounts \(x_0\) and \(y_0\) wishing to hedge the value of their initial position in the numéraire token \(Y\). The goal then is to replicate the value \(V(P)\) with options so that at option maturity, the payoff of the option portfolio corresponds to that of the liquidity provision. To do so, we condense Equation (7) into a single equation using the notation \((x)^+=\max(0,x)\):
| $$V(P) /\ell = P \ \left(\frac{1}{\sqrt{P}}-\frac{1}{\sqrt{P_U}} \right)^{+} - P \ \left(\frac{1}{\sqrt{P}} - \frac{1}{\sqrt{P_L}} \right)^{+} \nonumber\\ + \left(\sqrt{P}-\sqrt{P_L} \right)^{+} - \left(\sqrt{P}-\sqrt{P_U} \right)^{+}.$$ | $$(8)$$ |
Following Fukusawa et al. (2023) “Weighted Variance Swaps”, we assume that interest rates are zero.8 By the Carr-Madan Formula,19 any function \(f(x)\) with left derivative \(f'\) and \(f''\) existing as a generalized function can be represented as
| $$ f(x) = f(x^*) + f'(x^*)(x-x^*)\nonumber \\ + \int_0^{x^*} f''(k) \ \left(k-x \right)^{+} \mathrm{d} k + \int_{x^*}^\infty f''(k) \ \left(x-k \right)^{+}\mathrm{d} k$$ | $$(9)$$ |
(cf. Carr & Lee (2009) Remark 3.1 or Carr et al. (2021) p.3).20–22 The valuation makes no assumptions on the dynamics of the price process, other than \(P\) being a positive process, so that the hedge is “model-free”.
| $$ x \left(\frac{1}{\sqrt{x}} - \frac{1}{\sqrt{\eta}}\right)^+ = \frac{1}{2\sqrt{\eta}} (\eta-x)^+ - \frac{1}{4} \int_0^\eta k^{-\frac{3}{2}} (k-x)^+ \mathrm{d} k $$ | $$(10)$$ |
| $$ \left(\sqrt{x} - \sqrt{\eta}\right)^+ = \frac{1}{2\sqrt{\eta}} (x-\eta)^+ - \frac{1}{4} \int_\eta^\infty k^{-\frac{3}{2}} (x-k)^+ \mathrm{d} k $$ | $$(11)$$ |
[Proof] We use Equation (9), and set \(x^*=\eta \) and \(f(x)=\sqrt{x}-x/\sqrt{\eta}\). We have \(f'(x)= 1/(2\sqrt{x})-1/\sqrt{\eta}\) and \(f''(x)=-1/4 x^{-3/2}\). Hence,
| $$ \left(\sqrt{x}-\frac{x}{\sqrt{\eta}}\right) = - \frac{1}{2\sqrt{\eta}} (x-\eta) \nonumber\\ - \frac{1}{4} \int_0^{\eta} k^{-3/2} \ \left(k-x \right)^{+} \mathrm{d} k - \frac{1}{4} \int_{\eta}^\infty k^{-3/2} \ \left(x-k \right)^{+} \mathrm{d} k $$ | $$(12)$$ |
which we re-order and multiply by the indicator \(\mathbf{1}_{\{x<\eta\}}\) to get
| $$ \left(\sqrt{x}-\frac{x}{\sqrt{\eta}}\right)^+ = \frac{1}{2\sqrt{\eta}} (\eta-x)^+ - \frac{1}{4} \int_0^{\eta} k^{-3/2} \ \left(k-x \right)^{+} \mathrm{d} k.$$ | $$(13)$$ |
The derivation of (11) follows analogously and can be found in Deng et al. (2023).13
The value of the liquidity provision claim at terminal time \(T \) per unit of \(\ell\) equals
| $$ \mathbb{E}[V(P_T)]/\ell =- \frac{1}{4} \int_{P_L}^{P_U} k^{-\frac{3}{2}} (p(k) + c(k)) \mathrm{d} k\nonumber\\ + \frac{1}{2\sqrt{P_U}} \left(p(P_U)-c(P_U) \right) + \frac{1}{2\sqrt{P_L}} \left(c(P_L)-p(P_L) \right) $$ | $$(14)$$ |
where \(P_T\) is the price at terminal time \(T\), \(c(k)\) and \(p(k)\) are European call and put options with maturity \(T\) and strike \(k\). Alternatively, the second line could be represented with forward contracts \(1/(2\sqrt{P_U}) (P-P_U) + 1/(2\sqrt{P_L}) (P-P_L)\).
[Proof] We apply Lemma 3.1 to Equation (8).
| $$ V(P)/\ell \\= \frac{1}{2\sqrt{P_U}} (P_U-P)^+ - \frac{1}{4} \int_0^{P_U} k^{-\frac{3}{2}} (k-P)^+ \mathrm{d} k \nonumber\\$$ $$- \frac{1}{2\sqrt{P_L}} (P_L-P)^+ + \frac{1}{4} \int_0^{P_L} k^{-\frac{3}{2}} (k-P)^+ \mathrm{d} k \nonumber\\$$ $$+ \frac{1}{2\sqrt{P_L}} (P-P_L)^+ - \frac{1}{4} \int_{P_L}^\infty k^{-\frac{3}{2}} (P-k)^+ \mathrm{d} k\nonumber\\$$ $$- \frac{1}{2\sqrt{P_U}} (P-P_U)^+ + \frac{1}{4} \int_{P_U}^\infty k^{-\frac{3}{2}} (P-k)^+ \mathrm{d} k\nonumber\\$$ $$= - \frac{1}{4} \int_{P_L}^{P_U} k^{-\frac{3}{2}} (k-P)^+ \mathrm{d} k - \frac{1}{4} \int_{P_L}^{P_U} k^{-\frac{3}{2}} (P-k)^+ \mathrm{d} k\nonumber\\$$ $$+ \frac{1}{2\sqrt{P_U}} ((P_U-P)^+ - (P-P_U)^+) \nonumber\\$$ $$+ \frac{1}{2\sqrt{P_L}} ((P-P_L)^+ - (P_L-P)^+). $$ | $$(15)$$ |
Taking expectations under the risk-neutral measure and applying put-call parity we have
| $$ \mathbb{E}[V(P_T)/\ell] = - \frac{1}{4} \int_{P_L}^{P_U} k^{-\frac{3}{2}} p(k) \mathrm{d} k - \frac{1}{4} \int_{P_L}^{P_U} k^{-\frac{3}{2}} c(k) \mathrm{d} k\nonumber\\ + \frac{1}{2\sqrt{P_U}} (P-P_U) + \frac{1}{2\sqrt{P_L}} (P-P_L). $$ | $$(16)$$ |
Proposition 3.2 perfectly replicates the liquidity provider positions. Hence, shorting the replicating portfolio that consists of options \(H:=-\mathbb{E}[V(P_T)]\) (see Eq. (16)) hedges the liquidity provider position. Options on Deribit are margined in base currency (BTC for options on BTC-USD), and termed inverse options. The initial margin requirement is significant in relation to the liquidity provision size and therefore needs to be dollar-hedged as well, using a perpetual or dated future. The hedge portfolio hence consists of inverse options and a future.
In practice, options cannot be purchased at a continuum of strikes, and we approximate the hedge portfolio \(H\) with a Riemann integral and denote this approximation as \(\renewcommand{\hat}[1]{\widehat{#1}}\hat{H}\). The hedging strategy requires the available strikes, \(K_i\) for \(i=1,...,N\), to enclose the boundaries \(P_L\) and \(P_U\).23 We can approximate \(H/\ell\) as
| $$ \renewcommand{\hat}[1]{\widehat{#1}} \hat{H}/\ell = \frac{1}{2\sqrt{P_U}} \left(c(P_U) - p(P_U)\right) + \frac{1}{2\sqrt{P_L}} \left(p(P_L) - c(P_L) \right) \\\nonumber +\frac{1}{4} \sum_i^N \mathbf{1}_{\{K_i\geq P_L, K_i\leq P_U\}} K_i^{-\frac{3}{2}} (p(K_i) + c(K_i)) (r_i-l_i) $$ | $$(17)$$ |
where \(l_i = \max\left(P_l, (K_{i-1}+K_i)/2 \right)\), and \(r_i = \min\left(P_u, (K_i + K_{i+1})/2 \right)\). This hedge involves selling a put option with strike \(P_U\) and selling a call option with strike \(P_L\)—similar to a short “gut spread”—which earns the premium from the short call and from the short put. Writing options requires the seller to post margin.24 To dollar-hedge the BTC-margin, we can either resort to dated futures or perpetual futures margined in USD-tokens. Typically dated futures are subject to contango, and hence earn a carry.3 Perpetual futures typically trade close to spot and feature a funding rate. Funding rates are paid from the long to the short when spot trades below the perpetual price, and have historically been positive on average, see e.g., Zou (2022),2 meaning that the short position earns funding rates.
We wish to hedge the liquidity provision position detailed in Table 1, which has an initial value of $48,612 at a BTC price of $63,950. To do so, we use options with maturity 30 August 2024, entering the position on 19 July 2024.
Table 1. Liquidity Provision Position to Hedge. In practice, our choice of liquidity provision range (\(P_L\), \(P_U\)) is informed by the availability of options. The best liquidity is available for near at-the-money and out of the money puts and calls. In-the-money puts and calls typically have higher spreads and lower liquidity. We therefore use taker prices (ask price when buying, bid price when selling) when calculating the hedging costs, as detailed in Appendix 4. We set \(Y\) and, given the current BTCUSD price, the values for \(\ell\), \(X\), and \(V(P_0)\) are given by the definitions of a concentrated liquidity AMM. |
\(P_L\) | $59,000 | \(\ell\) | 2,503.95 | |
\(P_U\) | $69,000 | \(X\) | 0.369226 | |
\(Y\) | $25,000 | \(V(P_0)\) | $48,611.98 |
Table 2 presents the complete portfolio consisting of liquidity provision position and hedge for a maturity of 42 days. Appendix 4 provides more details on the construction of the hedge.
Table 2. Summary of LP Position and Hedge. This table shows that the expense for a dollar hedged liquidity provision position (in BTC and converted to USD), including a hedge of the initial margin provided in BTC with a 3x initial leverage. The market neutral portfolio amounts to a total capital expense of $211,556, of which the liquidity provision is $48,612. |
BTC | USD | |
Margin net of premia | 1.557 | $99,562 |
Premia long options | 0.472 | $30,195 |
LP | 0.760 | $48,612 |
Short Perpetual (3x) | 0.519 | $33,187 |
Expense | 3.308 | $211,556 |
4.1 Capital Efficiency—The capital expense at trade initiation for the entire portfolio corresponds to the margin requirement for the options sold net of the premia received (1.557 BTC) plus the premia paid for the long options (0.472 BTC) plus the LP position (0.760 BTC) plus the perpetuals margin (0.519), resulting in 3.308 BTC (see Figure 1).
The best liquidity for options is available for near at-the-money and out of the money puts and calls. In-the-money puts and calls typically have higher spreads and lower liquidity. We are buying put and call options with strikes between \(P_L\) and \(P_U\) and are therefore trading-off hedge accuracy for hedging costs.25 Figure 3 pictures the hedge accuracy by comparing the constructed replicating portfolio (the negative value of the hedge at maturity) with the value of the LP pool at maturity. The net positive option premia are achieved because the proceeds from selling an out of the money put option with strike \(P_L\) and selling an out of the money call option with strike \(P_U\) exceeds the costs for the put and call options bought with strikes between \(P_L\) and \(P_U\) (using taker prices).
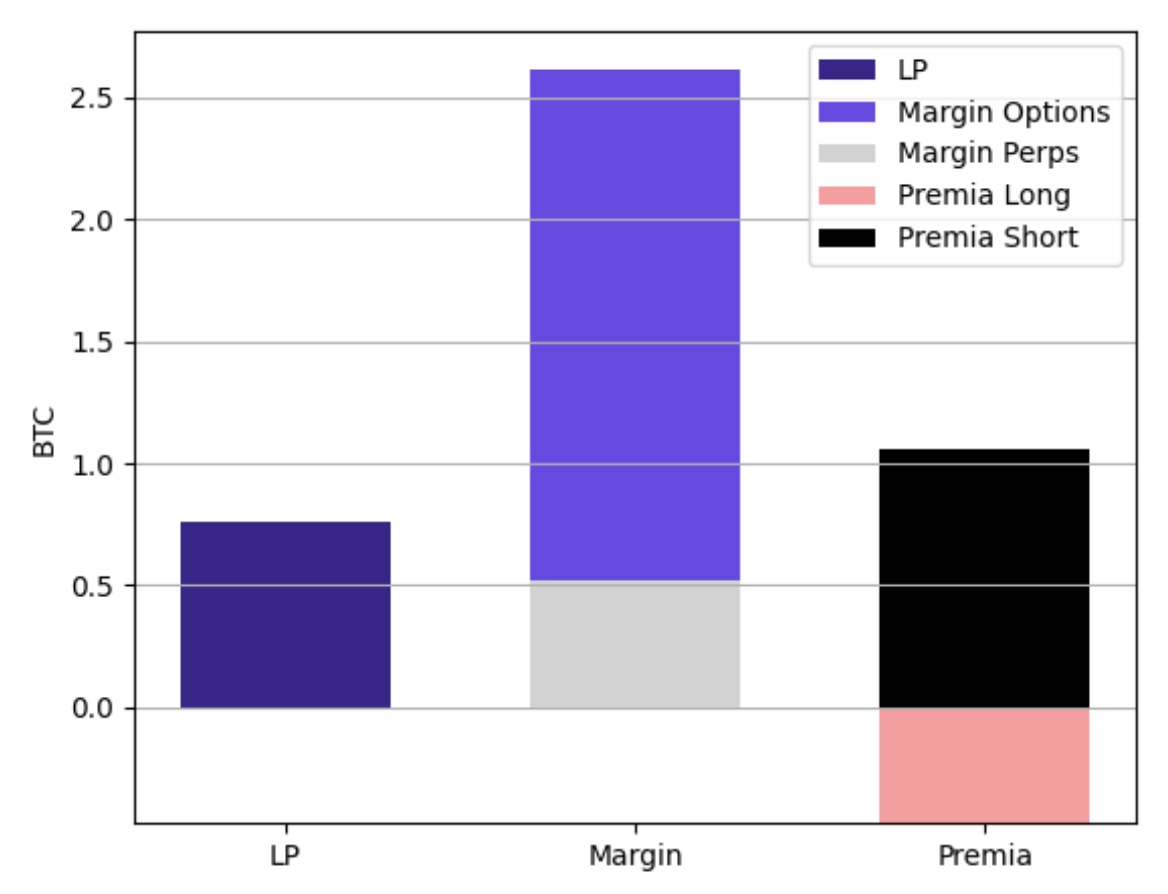
Fig. 1. The delta-neutral liquidity provision strategy involves liquidity provision (“LP”), selling options (“Premia Short”), buying options (“Premia Long”), margin for the options sold (“Margin Options”), and margin for hedging the margin in BTC assuming a 3x leverage. |
To assess the amount we receive at maturity, note that we receive back the entire margin expended for the perpetuals. The reason is that the P&L that is added to the perpetual margin (subtracted when at loss), equals the negative P&L in the options margin that we hedge. Similarly, the margin in the options can be recovered in full due to the corresponding P&L in the liquidity pool position. Therefore the amount we receive at maturity corresponds to the dollar value of the margin at trade initiation $200,446 (consisting of the options margin of $167,259 and the perpetuals margin of $33,187), plus the hedged value of the LP position ($48,612) plus proceeds from funding rates and trading fees from the LP position. Note that we have already subtracted the option premia received from the capital expended.
As a consequence, to assess earnings, our metric is the income from LP trading fees and perpetuals funding rate, relative to the expense at initiation. We now analyze this metric for different scenarios of funding rates and trading fee income. DefiLlama shows historical annualized yields for WBTC-USDC, from which we can infer that yields of 3%-15% are realistic assumptions. Perpetual funding rates are typically positive and hover around 1 basis point (0.01% for an 8-hour period).26 From Deribit and The Block, we can see that over the course of 2024 funding rates are mostly positive and we consider annualized funding rates from -5% to 15% realistic assumptions for our assessment.27 From these yield scenarios, we calculate the resulting portfolio yield in Figure 2. We can see that the portfolio yield can go negative if perpetual funding rates turn negative. Note that we could lock-in the carry by purchasing a dated future instead.
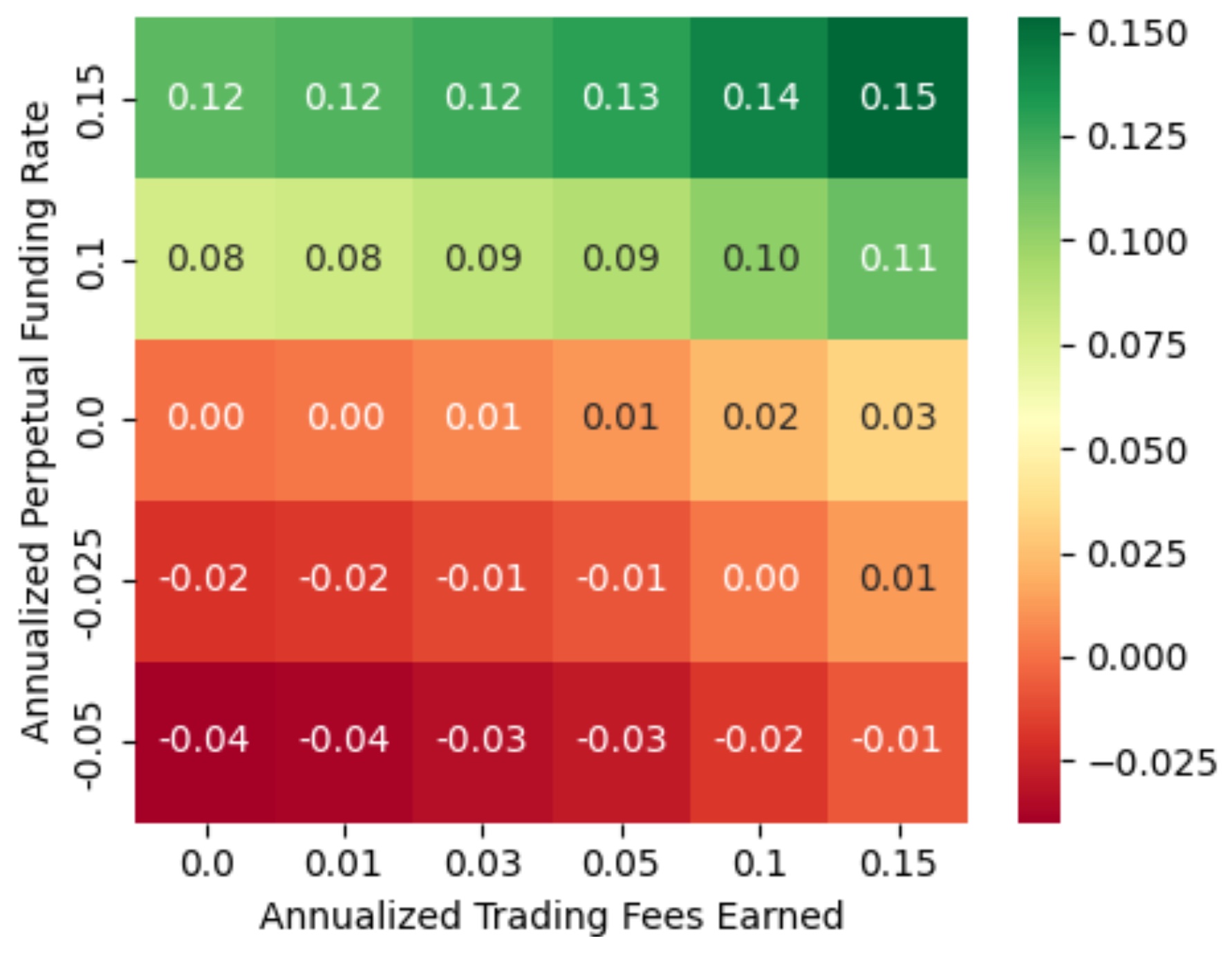
Fig. 2. Annualized yield income relative to the capital deployed for different scenarios. The plot shows different assumptions for annualized yields from trading fees of the LP position (x-axis), different assumptions for annualized perpetual funding rates, resulting in a return on the capital deployed. For example, if the annualized funding rate is 10% and the annualized trading fees add up to 5% over the duration of the trade, the amount earned relative to the capital expended equals an annualized 9%. Note that, if we were to use a dated future, the carry would be locked-in from the start. |
4.2 Risk Management—Maintenance margin requirement for the option portfolio and the short future have to be met during the entire holding duration of the position. Even though we have a static hedge, the strategy calls for active risk management. First, the margin for the short future needs to be increased as the price of the underlying soars, or the notional can be reduced. Second, the margin of the options portfolio needs to be maintained.
Deribit allows for portfolio margins that are limited by the “maximal loss”, a figure calculated with the Black-Scholes model incorporating stressed parameters.28 A proxy for the maximal loss is the intrinsic value of the portfolio; if the loss in the intrinsic value is limited, so is the point in time estimate using Black-Scholes. Figure 3 shows that the portfolio value no longer increases above the upper limit \(P_U\). At prices above \(P_U\) the LP position consists of USDC only. Therefore, the option portfolio’s intrinsic loss is bounded by the value of the option portfolio at \(P_U\) and additional funds for maintaining the option portfolio are limited.
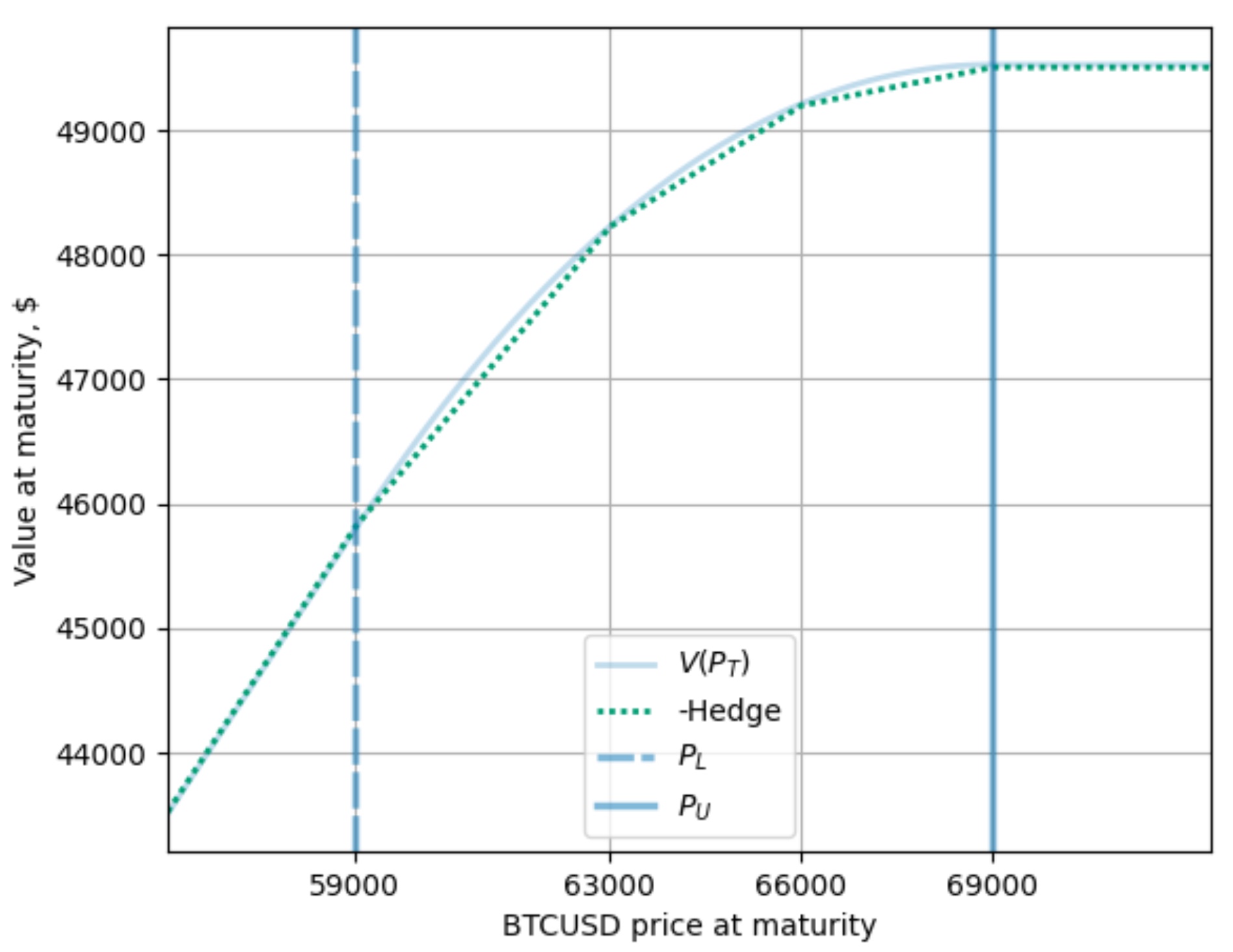
Fig. 3. This plot shows the liquidity provision value at maturity for a particular choice of lower and upper limits at \(P_L=\$59,000\) and \(P_U=\$69,000\). The dotted line depicts the negative end-of-period value of a hedge portfolio with 4 short straddles, a synthetic long at \(P_L\) and a synthetic short at \(P_U\). The underlying options are detailed in Appendix Table 4. We can see that the negative hedge closely approximates the liquidity provision value at maturity, rendering the hedge effective. |
We derived a hedge portfolio for market neutral liquidity provision in concentrated liquidity pools. The hedge is derived in a “model-free” manner, that is, making no assumption on the underlying price process other than it being a positive process. In the empirical part of this paper, we find that only a few options are sufficient to provide an accurate hedge. The availability of options in the current market environment severely restricts the price-range, maturity, size, and choice of tokens for the liquidity provision position. The initial margin required for the options portfolio is about twice the amount of the liquidity provision position. Due to the large amount of margin compared to the liquidity provision position, the margin held in base-currency requires a hedge, too. Interestingly, the hedge portfolio is an additional source of earnings. That is, the net premia for the option portfolio are positive, and the margin hedge typically earns a futures carry. The economic intuition for the negative hedge costs is that the option portfolio forgoes the upside when prices increase beyond the upper limit of liquidity provision (\(P_U\)), similar to a covered call. Even though we have a static hedge at hand, the strategy requires dynamic risk management for the maintenance margin requirement.
We thank the Deribit help desk for support on understanding margin requirements, and we are grateful to the participants of CFC St. Moritz 2024 for valuable questions, comments, and discussions. We are also thankful for the constructive comments of the referees.
Both authors contributed to the conceptualization and structure of the paper. BM derived the replicating portfolio, gathered the data from Deribit, analyzed the relevant trading conditions and requirements, and developed the code for implementing the hedging strategy. MW provided a review of and context with the relevant literature, as well as a thorough review and suggestions on all sections. Both authors contributed to the analysis and interpretation of the results.
The authors declare that they have no known conflicts of interest as per the journal’s Conflict of Interest Policy.
1 Clark, J. “The Replicating Portfolio of a Constant Product Market with Bounded Liquidity.” SSRN (2021) (accessed 9 November 2024) https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3898384.
2 Zou, J. “Exploring Arbitrage Opportunities between the BTC Spot and Futures Market based on Funding Rates Mechanism.” In 2022 7th International Conference on Financial Innovation and Economic Development (ICFIED 2022) Atlantis Press 1923–1928 (2022) https://www.atlantis-press.com/proceedings/icfied-22/125972028.
3 Schmeling, M., Schrimpf, A., Todorov, K. “Crypto Carry.”BIS Working Papers (accessed 9 November 2024) https://www.bis.org/publ/work1087.pdf.
4 Mohan, V. “Automated Market Makers and Decentralized Exchanges: A DeFi Primer.” Financial Innovation 8.1 20 (2022) https://jfin-swufe.springeropen.com/articles/10.1186/s40854-021-00314-5.
5 See: https://balancer.fi/ (accessed 24 November 2023).
6 See: https://curve.fi/ (accessed 24 November 2023).
7 Milionis, J., Moallemi, C. C., Roughgarden, T., Zhang, A. L. “Automated Market Making and Loss-Versus- Rebalancing.” arXiv (2023) (accessed 9 Noember 2024) https://arxiv.org/abs/2208.06046.
8 Fukasawa, M., Maire, B., Wunsch, M. “Weighted Variance Swaps Hedge Against Impermanent Loss.” Quantitative Finance 23.6 901–911 (2023) https://www.tandfonline.com/doi/full/10.1080/14697688.2023.2202708.
9 Fukasawa, M., Maire, B., Wunsch, M. “Model-Free Hedging of Impermanent Loss in Geometric Mean Market Makers.” (2023) (accessed 9 November 2024) https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4397904.
10 Milionis, J., Moallemi, C. C., Roughgarden, T. “Automated Market Making and Arbitrage Profits in the Presence of Fees.” arXiv (2023) (accessed 9 November 2024) https://arxiv.org/abs/2305.14604.
11 Sepp, A., Lipton, A., Lucic, V. “Unified Approach for Hedging Impermanent Loss of Liquidity Provision.” SSRN (2024) (accessed 9 November 2024) https://ssrn.com/abstract=4887298.
12 Clark, J. “The Replicating Portfolio of a Constant Product Market.” SSRN (2020) (accessed 9 Novemeber 2024) https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3550601.
13 Deng, J., Zong, H., Wang, Y. “Static Replication of Impermanent Loss for Concentrated Liquidity Provision in Decentralised Markets.” Operations Research Letters 51.3 https://www.sciencedirect.com/science/article/abs/pii/S0167637723000445.
14 At the time of writing, this type of AMM has been forked 45 times, source: https://defillama.com/forks/.
15 The smart contract tracks \(L_i\) and \(\sqrt{P}\), not \(x^{(v)}\) and \(y^{(v)}\). The trading function can be reformulated accordingly to replace \(x^{(v)}\) and \(y^{(v)}\).
16 Adams, H., Zinsmeister, N., Salem, M., Keefer, R., Robinson, D. “Uniswap v3 Core Whitepaper.” Uniswap (2021) (accessed 9 November 2024) https://uniswap.org/whitepaper-v3.pdf.
17 For the analysis of impermanent loss of Uniswap V2 type AMMs one typically assumes trading fees are held outside the pool. In the presence of fees, the dynamics of the pool are different. See Mohan (2022) p.22, and cf. Fukasawa (2023) Section 5.8.
18 Lambert, G., Kristensen, J. “Panoptic: The Perpetual, Oracle-Free Options Protocol.” arXiv (2023) (accessed 9 November 2024) https://arxiv.org/abs/2204.14232.
19 Bossu, S. Advanced Equity Derivatives. Hoboken, New Jersey: John Wiley & Sons, Inc (2004).
20 Carr, P., Lee, R. “Robust Replication of Volatility Derivatives.” (2009) (preprint) (accessed 9 November 2024) https://math.uchicago.edu/~rl/rrvd.pdf.
21 Carr, P., Lee, R., Lorig, M. “Robust Replication of Volatility and Hybrid Derivatives on Jump Diffusions.” Mathematical Finance 31.4 1394–1422 (2021) https://doi.org/10.1111/mafi.12327.
22 For example, Equation (9) is true in this sense for the “hockeystick” payoff functions of plain vanilla European put or call options.
23 The grid of ranges for liquidity provision is also discrete (see Appendix A) and hence does not exactly match the available strikes. For the study at hand, the relative error between chosen strikes and available price ranges is small (a relative error of 0.02% and 0.04%), so we assume that \(P_U\) and \(P_L\) are in the set of available liquidity provision ranges.
24 On Deribit, the initial margin for short options depends on the “option mark price” and the “underlying mark price.” For a given strike, maturity, call or put, the option mark price usually corresponds to the average of the best bid and best ask price (see “Deribit Options Knowledge Base”).29 The underlying mark price corresponds to the mark price of the future of the underlying instrument with the same maturity that is calculated as the underlying instrument price (e.g., Deribit BTC index) plus a 30 seconds EMA of the futures market price net of the index price (see “Deribit Futures Knowledge Base”).30
25 We are reporting taker prices, i.e., ask prices when buying options.
26 See: https://defillama.com/yields?token=WBTC&project=uniswap-v3&show7dBaseApy=true.
27 See: https://www.deribit.com/statistics/BTC/funding-rate, https://www.theblock.co/data/crypto-markets/futures (accessed 29 September 2024).
28 See: https://www.deribit.com/kb/portfolio-margin.
29 No Author. “Deribit Options Knowledge Base.” Deribit (2023) (accessed 30 December 2023) https://www.deribit.com/kb/options.
30 No Author. “Deribit Futures Knowledge Base.” Deribit (2023) (accessed 30 December 2023) https://www.deribit.com/kb/futures.
The price ranges for liquidity providers are discrete and not spaced equally. Discrete prices are determined as P = 1.0001t, where t is the discrete tick index. Different fee tiers can have different tick spacings. If the tick spacing is 1, liquidity can be placed at every tick. If tick spacing is 60, liquidity can only be placed at t equal to integer multiples of 60. For example, the 0.3% fee tier of WBTC/USDC on Uniswap has a tickspacing of 60, see https://etherscan.io/address/0x99ac8cA7087fA4A2A1FB6357269965A2014ABc35#readContract.
Table 3 shows that concentrated liquidity DEXs are the most prominent type of DEXs at the time of writing, by an order of magnitude.
Table 3. Seven day trading volume (billion USD) and total value locked (TVL, billion USD) as of July 21, 2024. Source: https://defillama.com/dexs |
Venue | 7D Volume | TVL | Type |
Uniswap v3 | 11.31 | 3.48 | Concentrated Liquidity |
PancakeSwap v3 | 2.22 | 0.22 | Concentrated Liquidity |
Uniswap v2 | 1.98 | 2.36 | Constant Product Market Maker |
Curve DEX | 1.24 | 0.06 | Hybrid Function Market Maker |
Balancer V2 | 0.37 | 0.06 | Constant Mean Market Maker |
We differentiate the pool value function, Equation (7), with respect to the price to get the position delta:
| $$ \frac{\partial V(P)}{\partial P} = \left\{ \begin{array}{ll} \ell (\frac{1}{\sqrt{P_L}}-\frac{1}{\sqrt{P_U}}) & P < P_L \\ \ell \left( \frac{1}{\sqrt{P}}-\frac{1}{\sqrt{P_U}} \right) & P_L < P < P_U \\ 0 & P > P_U. \end{array} \right. $$ | $$(18)$$ |
The delta hedge, \(-\partial V(P)/\partial P\), corresponds to shorting the amount of token \(x\) that the liquidity provider owns for a given price \(P\), and therefore Equation (18) coincides with Equation (5). The position’s Gamma is given by
| $$ \frac{\partial^2 V(P)}{\partial P^2} = \left\{ \begin{array}{ll} -\frac{\ell}{2 P^{3/2}} & P_L < P < P_U \\ 0 & P \not\in [P_L, P_U] \\ \end{array} \right. $$ | $$(19)$$ |
Figure 4 shows an example of the liquidity provision value as a function of the price, the delta, and the token composition.
Some exchanges allow dedicated market makers to write options, but not regular clients (Binance, for example). Deribit quotes their European BTCUSD options in BTC.
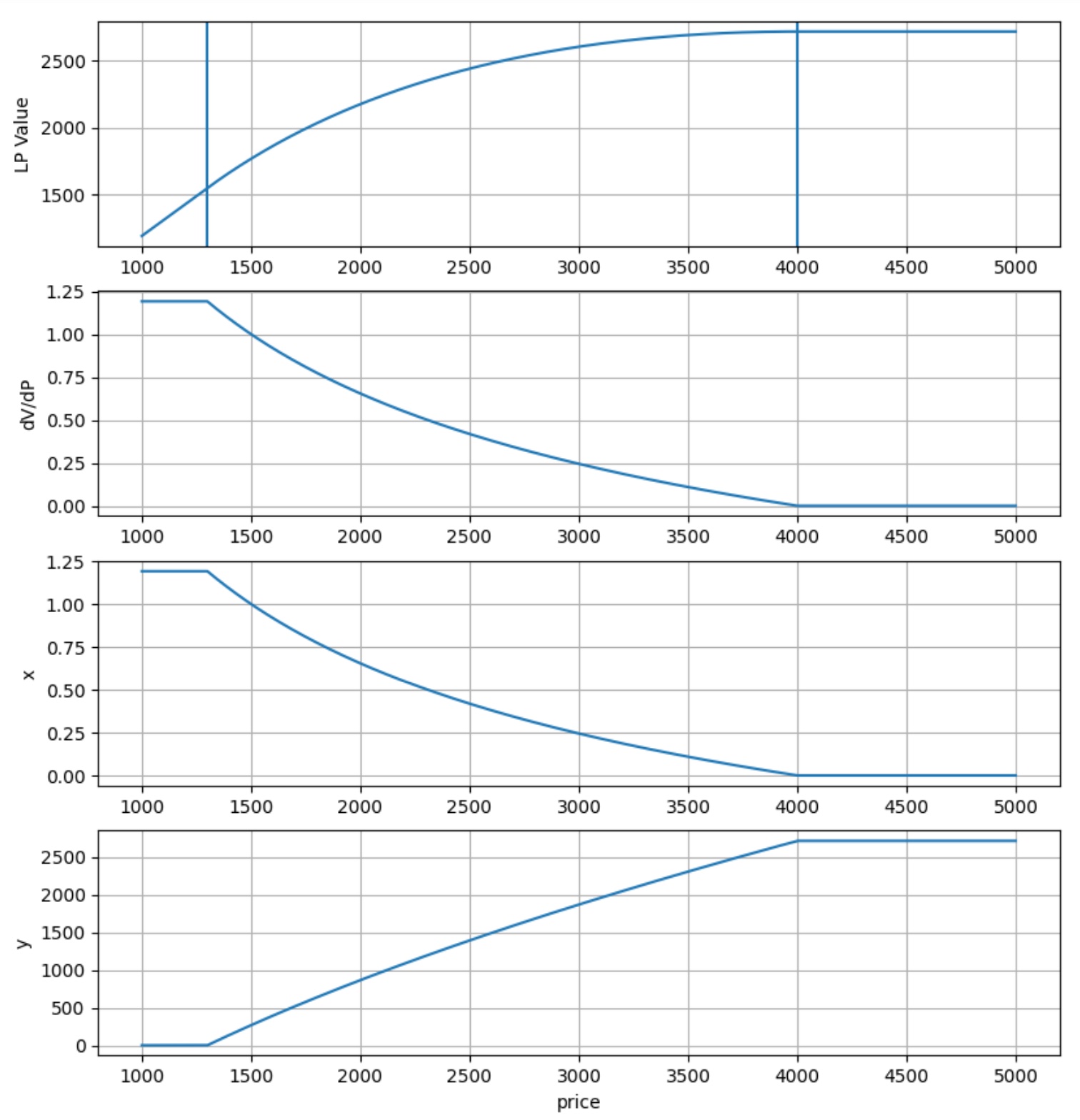
Fig. 4. LP value, the price delta, and the token composition as a function of the price. The vertical lines denote the lower and upper bounds of the concentrated liquidity provision. |
The minimal position size is 0.1 contracts (corresponding to 0.1 BTC), and the tick size is 0.0001. The minimal position size only allows accurate hedges for liquidity provision portfolios starting at around $25,000 at prices prevalent at the time of writing. Table 4 presents the hedge portfolio in detail. We calculate the amount for each call and put option required according to the equation for \(\hat{H}\). We use “taker prices”, that is, when we write options (calls for \(P_L\) and puts for \(P_U\)), we use the bid price; otherwise, we use ask prices. For the margin requirement we are assuming standard position margins, for which each position has its margin requirements calculated separately. We want to sell in-the-money call and put options. Deribit requires the following margin,
Max (Max (0.15 - OTM Amount/Underlying Mark Price, 0.1)
+ Mark Price of the Option, Maintenance Margin),
which reduces to 15% plus the option mark-price times the number of contracts. Long options do not require any margin.
Table 4. Hedge Portfolio. The hedge portfolio consists of options struck at four different prices from $59,000 to $69,000 on 19 July 2024 with maturity 30 August 2024. Figure 3 depicts the hedge accuracy for this choice. The premia are ask prices, unless we write the option, in which case we use bid prices (italic), denoted in BTC. The amount of calls/puts is denoted in the number of contracts (1 contract has one underlying BTC as an asset) and calculated according to the hedge approximation \(\hat{H}\) described in this paper. The costs are calculated as the amount times the corresponding premium, a number in BTC. The hedge portfolio is a net seller of options that results in 0.586 BTC (=0.347+0.239) in income. However, note that there is a considerable amount of margin that has to be posted for the short positions, so the premia earned are used as margin collateral until maturity. |
Strike | Put Premium | Call Premium | Amount Call | Amount Put | Cost Call | Cost Put |
59000 | 0.0350 | 0.122 | -5.07 | 5.24 | -0.618 | 0.183 |
63000 | 0.0610 | 0.0905 | 0.14 | 0.14 | 0.013 | 0.008 |
66000 | 0.0865 | 0.0685 | 0.11 | 0.11 | 0.008 | 0.010 |
69000 | 0.095 | 0.052 | 4.82 | -4.64 | 0.251 | -0.440 |
Sum | -0.347 | -0.239 |
